Keep Sharp

Intelligent Scissor

This computer vision project is to realize the function of cutting out the objects you are interested inside a picture and then save it as another picture which has transparent background except the cut out objects. You can download the code from here. Here is an example of Lena picken out from that "You know what i am talking about" iamge:

The idea is simple, just need to understand following concepts:

Pixel Node

one pixel becomes a 3by3 matrix with the original pixel in the center and other 8 additional pixel saves the link cost in that direction.

so the Pixnode picture will be 9 times larger as the original picture.

Cost Function

For vertical or horizental link:

$$ D_{link1} = \frac{|Img(i+1,j)-Img(i,j-1)|}{\sqrt{2}} $$

For diagonal link:

$$ D_{link0} = \frac{|Img(i,j-1)+Img(i+1,j-1)-Img(i,j+1)-Img(i+1,j+1)|}{4} $$

Define \(D_{max}\) as the maximum link cost among all the links in the picture. Then the final cost function we will use later can be defined as:

$$ C_{link} = (\sqrt{maxD}-\sqrt{D_{link}})*length_{link} $$

where \(length_{link}\) is 1 for horizental and vertical links, 0 for diagonal links. The reason i put \(\sqrt{}\) here is because

$$ \frac{\sqrt{y_2}-\sqrt{y_1}}{\sqrt{y_1}-\sqrt{y_0}} \lt \frac{y_2-y_1}{y_1-y_0} \qquad where \quad y_0 \lt y_1 \lt y_2 $$

Above is for the calculation of 1 color channel, if you have an RGB image, each link's cost can be

$$ D_{link} = \sqrt{\frac{DR_{link}^2+DG_{link}^2+DB_{link}^2}{3}} $$

Minimum Cost Path

Because the link along the edge has the minimum link cost (\(C\) not \(D\)), so from a source point to a destination point, if we find its minimum cost path, it will try to follow the edges, this is the idea. Just use Dijkstra Algorithm with datastructure of Fibonacci Heap to find the minimum cost path.

Usage

After loading a picture, you can zoom in zoom out and drag by right click, it will be shown like this

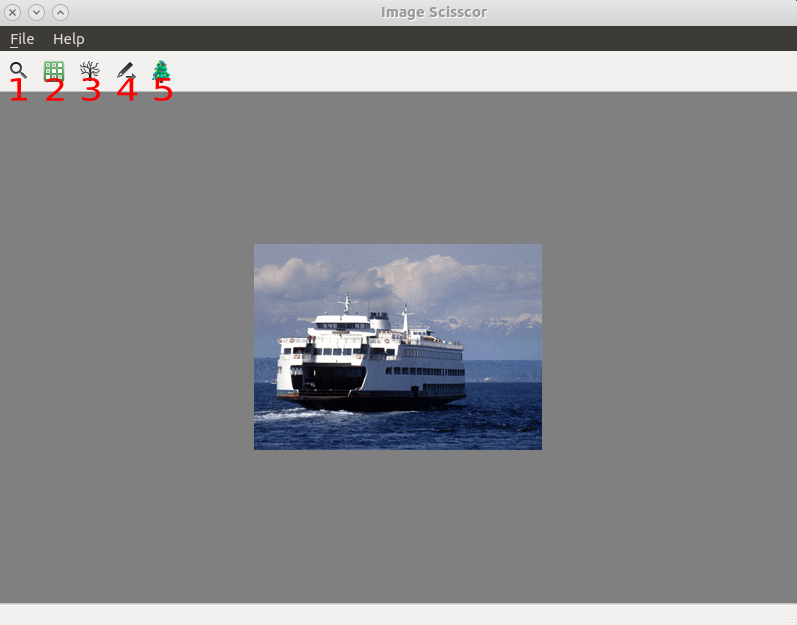
  • 1: show pixel node graph
  • 2: show cost graph

Pixel node graph and cost graph are calculated when the picture is loaded. Pixel node graph:

Cost Graph:

  • 3: show path tree
  • 4: show minimum path from seed to cursor
  • 5: show animation of Dijkstra Algorithm

By clicking on the picture, you can put a seed there. Before the first click of the picture, clicking 3 4 5 will not response because there is no seed yet. When you click on the picture, the path tree is generated. Here is a path tree (Can you find the seed node?):

when you click again on the image, the seed is changed, you have to close the opencv windown and click 3 again to see the updated path tree.

5 is a like a checkbox button, when it's on, everytime you click on the picture, it will show the animation of generating the path tree.

The above animation can be shown in Chrome.

After clicking 4 or press "F", you will enter the mode of scissoring the part you want. Put seed by clicking on the image, and move your mouse, you will see

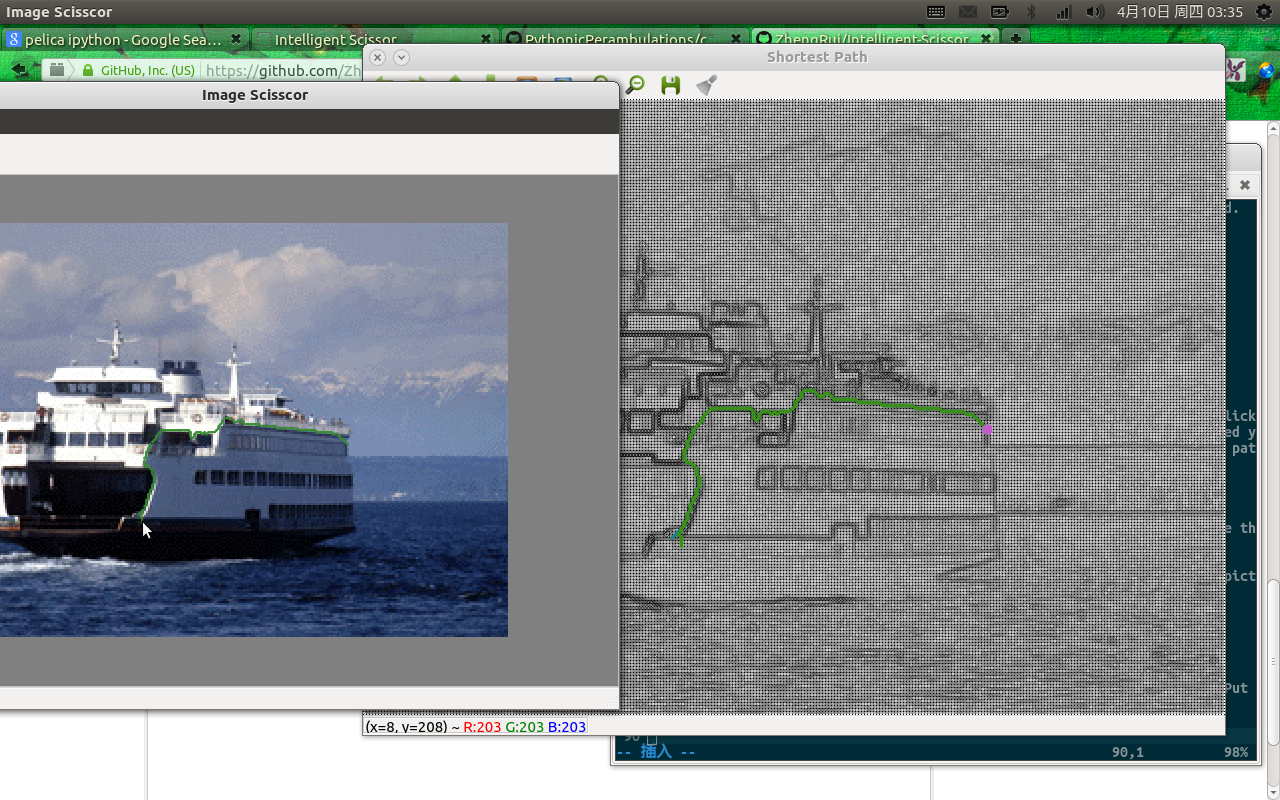
the path will show both in QGraphicsView and opencv window. There are two lines, green line is minimum cost path from seed to the cursor, blue line is minimum cost path from seed to a pixel which is in a certain range of the cursor but has the minimum cost link within the range. You can choose cursor as next seed point by clicking or you can choose the blue ends as next seed point by "Ctrl"+click.

You can pause scissoring mode by clicking 4 or press "F", then you can select the path segments and delete the selected segment by pressing "D".

Note: Better delete with reverse order, from nearest to oldest segments, other wise when "save" in last step, it will have problem because the polygon is formed assumed that the segments is clock wise or counter clock wise sorted. Of course i could sort the segments before forming the polygon so that the segment can be deleted arbitrarily, but now i haven't implement the sort function.

You can press "F" or click 4 to enter scissoring mode again, and at last if you think it should be closed, press "Ctrl"+"B", the cursor will go back to the first seed point. Then press "F", quit from the scissoring mode and you can save the cutted part.

Here is a composite

Comments